-
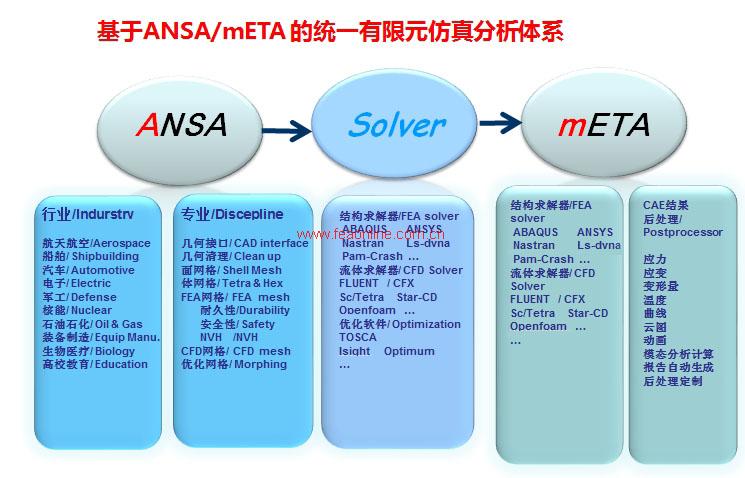
行业解决方案
12年的专业CAE咨询服务经验,超过1000个项目的丰富经验积累。
- 航天航空
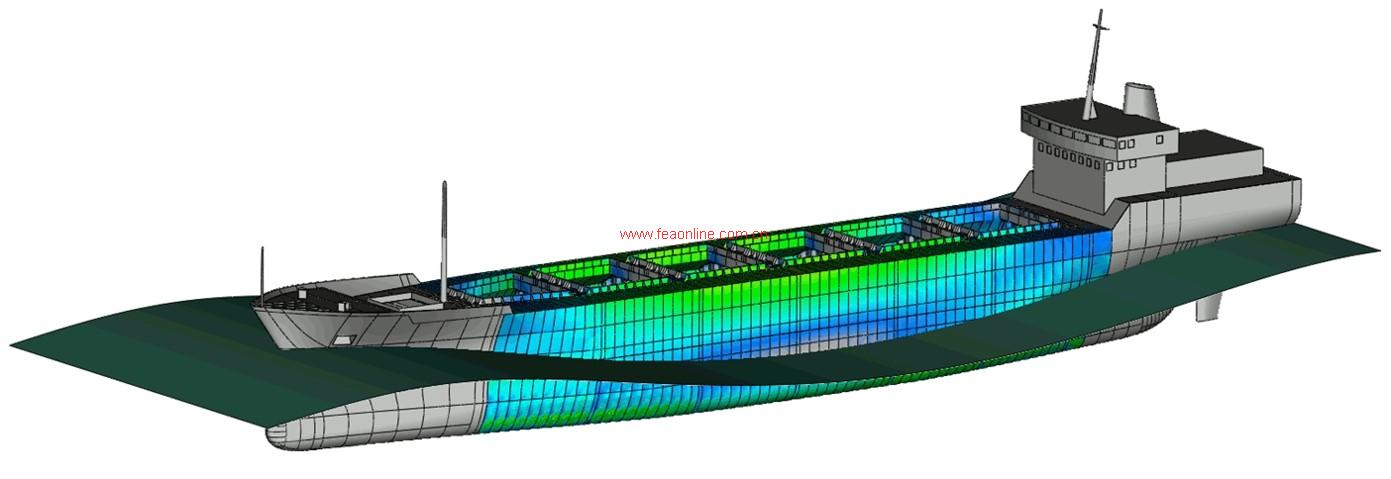
- 船舶海工
- 风能风电
- 汽车车辆
- 电子电器
- 石油石化
- 土木建筑
- 能源装备
- 生物医疗
- 电机设计
-
学科解决方案
12年的专业CAE咨询服务经验,超过1000个项目的丰富经验积累。
- 前处理
- 后处理
- CFD分析
- 多体运动学分析
- 疲劳分析
- CAE优化分析
- 注塑分析
- FEA分析
- 电机电磁分析
-
CAE专题解决方案
12年的专业CAE咨询服务经验,超过1000个项目的丰富经验积累。
- 复合材料分析
- 焊接分析
- 车身电泳烤漆分析
- 舱内热舒适性分析
- 流固耦合分析
- 动网格分析
- 地震响应分析
- 多参优化分析
- 拓扑优化分析
- 整车 CFD 分析
- 整车 NVH 分析
- 整车动力学分析
- 整车碰撞安全分析
- 整车耐久性分析
- 橡胶产品分析
- 汽车空调 HAVC
- 注塑成型分析
- 爆炸冲击分析
- 损伤与断裂分析
- 芯片封装分析
- 跌落碰撞分析
- 车辆发动机分析
有限元法(FEA)是随着电子计算机的使用而发展起来的一种有效的数值计算方法。这种方法大约起源于20世纪50年代的飞机结构矩阵分析。而随着计算机软硬件水平的提高,求解离散系统问题变得容易起来,即使对于连续系统,只要单元数目选择合适也是如此。工程上处理连续体问题的方法一般是将连续系统离散化,使连续系统变成离散系统,从而可以采用解决离散系统问题的方法,用计算机进行处理。这种离散当然仍带有近似性,但是,当离散变量的数目很大时,离散系统的分析结果可以逼近真实的连续解。有限元法就是用于求解连续系统问题的一种离散化方法。
有限元方法将一个物体划分为由许多小的单元(有限单元)组成的离散系统,这些单元以多个节点相互连接,这个过程叫做离散化。通过建立每一个有限单元的方程,并组合这些方程而得出对应整个物体的问题的解答。目前,有限元法已成为工程设计中不可或缺的一种重要方法,在结构问题分析方面应用的尤为广泛,例如大型结构受力分析、变形分析、振动分析;在非结构问题分析方面较典型的包括失效分析、传热分析、电磁场分析、流体流动(包括通过多孔材料的渗流)分析等;甚至于在某些生物力学工程问题的分析中也使用的越来越多,例如人的脊柱、头骨、股关节、颌面移植、树胶牙齿移植、心脏和眼的分析等等。
l有限元法的优点
有限元法已应用于大量的工程问题分析,既包括结构问题,也包括非结构问题,该方法具有很多优点,这包括:
◆ 该方法建立于严格的理论基础上具有良好的可靠性;
◆ 能够方便地模拟不规则形状的结构;
◆ 可以毫无困难地处理一般的荷载条件;
◆ 由于单元方程是单个建立的,因此可以模拟由几种不同材料构成的物体;
◆ 可以处理数量不受限制的和各种类型的边界条件;
◆ 单元的尺寸大小可以变化,必要时可使用小单元;
◆ 改变有限元模型比较容易,花费不大;
◆ 可包括动态作用;
◆ 可处理大变形和非线性材料带来的非线性问题。
l有限元法的基本思想
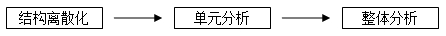
有限元法的基本思想可以用下述几点进行说明:
a)假想将连续系统划分成有限数目的单元,单元之间只在数目有限的节点处相互连接,以一个单元集合体代替原来的连续系统。在节点上引进等效载荷(或其它边界条件),代替实际作用于连续系统上的外载荷(或其它边界条件)。这一处理称为“结构离散化”。
b)对每个单元按一定的规则(由物理学关系或函数关系)建立求解节点上的未知量(比如位移)与节点上的已知量(比如作用力)之间的关系(力—位移、热量—温度、电压—电流等)。这一处理称为“单元分析”。
c)将所有单元的这种特性关系按一定条件(变形协调条件、连续条件或变分原理及能量原理)集合起来,引入边界条件,构成一组以节点未知量(位移、温度、电压等)为变量的代数方程组,求解之得到有限个节点的待求变量。这一处理称为“整体分析”。
所以,有限元法实质上是将具有无限个自由度的连续系统,理想化处理为只有有限个自由度的单元集合体,使问题转化为适合于数值求解的结构型问题。